Mastering The Percent Error Formula: Your Guide To Accuracy
Understanding the Essence of Percent Error
Before diving into the mechanics of the percent error formula, it's essential to grasp its fundamental meaning and purpose. This metric serves as a bridge between an observed or estimated value and a known, true value, providing a clear, percentage-based representation of their disparity.What is Percent Error?
Percent error, often referred to as percentage error, is a statistical measure that quantifies the relative size of the difference between an experimental or estimated value and a theoretical actual value. It's an expression of how close a measured value is to a true value, presented as a percentage. In essence, it tells you how significant an error is in relation to the correct answer. For instance, if you're trying to measure the length of a table, and your measurement is slightly off, the percent error will tell you what percentage of the table's actual length that deviation represents. This makes it a powerful tool for comparing the accuracy of different measurements or experiments, even if they involve vastly different scales. It's a statistic that compares an estimate to a correct value and expresses the difference as a percentage.Why is Percent Error Important?
The significance of percent error extends far beyond academic exercises. It's a cornerstone of reliability and quality control in countless fields. Here's why it holds such importance: * **Quantifying Accuracy:** It provides a standardized way to quantify the accuracy of a measurement or an experiment. Instead of just knowing there's a difference, you know the *relative* magnitude of that difference. * **Benchmarking and Comparison:** Percent error allows for easy comparison of accuracy across different experiments, methods, or even different individuals performing the same task. A 5% error in one experiment can be directly compared to a 5% error in another, regardless of the absolute values involved. * **Identifying Sources of Error:** A high percent error often signals that there might be significant systematic errors in an experimental setup, measurement technique, or estimation process. It prompts further investigation into potential flaws. * **Quality Control:** In manufacturing, percent error is critical for ensuring products meet precise specifications. A small deviation could lead to product failure, safety hazards, or significant financial losses. * **Scientific Validity:** In scientific research, reporting percent error is crucial for the validity and reproducibility of results. It helps other researchers assess the reliability of findings and replicate experiments. It is often used in science to report the difference between experimental values and expected values. * **Informing Decisions:** Whether it's in engineering, finance, or everyday life, understanding the potential error in an estimate or measurement helps in making more informed and robust decisions. Understanding why percentage error is important in scientific experiments and manufacturing processes underscores its role as a fundamental metric for precision and reliability.Deconstructing the Percent Error Formula
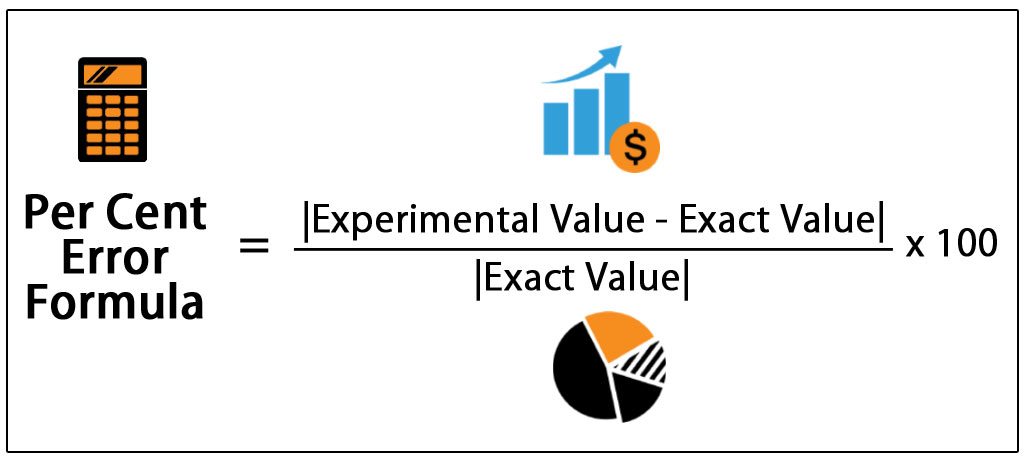
To truly master the percent error formula, we must understand its components and how they interact to yield a meaningful result. The formula itself is straightforward, yet each part plays a crucial role.The Core Formula Explained
The percent error formula calculates the absolute value of the difference between the measured value and the actual value, which is then divided by the actual value, and finally multiplied by 100 to express it as a percentage. Here's the formula: **Percent Error = (|Experimental Value - Actual Value| / Actual Value) × 100%** Let's break down each term: * **Experimental Value (or Measured/Estimated Value):** This is the value you obtained through your experiment, measurement, or estimation. It's your observed data. * **Actual Value (or True/Theoretical/Known Value):** This is the universally accepted, correct, or precise value. It's the standard against which your experimental value is compared. * **Difference (|Experimental Value - Actual Value|):** This part calculates the absolute difference between your experimental value and the actual value. The vertical bars `| |` denote the absolute value, meaning any negative result from the subtraction is converted to a positive number. This is crucial because error is about magnitude, not direction (i.e., being 5 units above the actual value is considered the same magnitude of error as being 5 units below it). * **Division by Actual Value (/ Actual Value):** Dividing the absolute difference by the actual value converts the absolute error into a relative error. This step is vital because it contextualizes the error. A difference of 5 units is much more significant if the actual value is 10 than if it's 1000. * **Multiplication by 100% (× 100%):** This final step converts the relative error (a decimal or fraction) into a percentage, making it easier to understand and compare.Breaking Down Absolute Error and Relative Error
The percent error formula is built upon two foundational concepts: absolute error and relative error. Understanding these helps in appreciating the full scope of the percent error formula. * **Absolute Error:** The absolute error is simply the absolute difference between the measured value and the true value. It tells you the raw magnitude of the discrepancy, without regard for direction. **Absolute Error = |Experimental Value - Actual Value|** For example, if you measure a 10 cm line as 10.2 cm, the absolute error is |10.2 - 10| = 0.2 cm. If you measure it as 9.8 cm, the absolute error is |9.8 - 10| = |-0.2| = 0.2 cm. Absolute error is useful for understanding the raw deviation but doesn't tell you how significant that deviation is in context. Find out what is the absolute error, the relative error and how to deal with negative values. * **Relative Error:** The relative error takes the absolute error and divides it by the actual value. This gives you the error as a fraction or decimal of the true value. **Relative Error = Absolute Error / Actual Value = |Experimental Value - Actual Value| / Actual Value** Using the 10 cm line example, if the absolute error is 0.2 cm, the relative error would be 0.2 cm / 10 cm = 0.02. This dimensionless value provides context: it tells you the error is 2% of the actual value, even before multiplying by 100. Relative error is crucial because it allows for meaningful comparisons across different scales. Absolute, relative, and percent error are ways to measure the error of a measurement or calculation. They are the most common methods used to express accuracy.Step-by-Step Calculation of Percent Error
Calculating percent error is a straightforward process once you understand the formula. Let's walk through the steps with a practical example.Practical Steps to Apply the Formula
To calculate percentage error, use the formula mentioned above. Here are the steps listed below: **Step 1: Identify the Experimental Value and the Actual Value.** Make sure you clearly distinguish between the value you measured or estimated (Experimental Value) and the true, accepted value (Actual Value). **Step 2: Subtract the Approximate Value from the Exact Value.** Calculate the difference between your experimental value and the actual value. `Difference = Experimental Value - Actual Value` Start off by subtracting one of the values from the other value in the equation. **Step 3: Take the Absolute Value of the Difference.** The result from Step 2 might be positive or negative. To ensure the error is always represented as a positive magnitude, take the absolute value. `Absolute Difference = |Experimental Value - Actual Value|` **Step 4: Divide that Number by the Exact Value.** Divide the absolute difference (from Step 3) by the actual value. This gives you the relative error. `Relative Error = Absolute Difference / Actual Value` **Step 5: Multiply the Result by 100 to Express as a Percentage.** Finally, multiply the relative error by 100 to convert it into a percentage. `Percent Error = Relative Error × 100%` **Example 1: Christian's Height Measurement** Christian attempted to measure his own height and came up with an estimated height of 58 inches. After a visit to the doctor, his actual height was measured at 60 inches. Let's calculate the percent error. * **Experimental Value (Estimated Height):** 58 inches * **Actual Value (True Height):** 60 inches 1. **Subtract:** 58 - 60 = -2 2. **Absolute Value:** |-2| = 2 3. **Divide:** 2 / 60 = 0.0333... 4. **Multiply by 100:** 0.0333... × 100 = 3.33% So, Christian's percent error in measuring his height was approximately 3.33%. **Example 2: William's Car Purchase** William wants to buy a new car for his son. Due to the pandemic, the estimated increased price at which the car is available is 130,000 dollars, while the actual value of the car is 100,000 dollars. Let's find the percent error in the estimated price. * **Experimental Value (Estimated Price):** $130,000 * **Actual Value (Actual Price):** $100,000 1. **Subtract:** $130,000 - $100,000 = $30,000 2. **Absolute Value:** |$30,000| = $30,000 3. **Divide:** $30,000 / $100,000 = 0.3 4. **Multiply by 100:** 0.3 × 100 = 30% The percent error in the estimated car price is 30%. This highlights a significant deviation from the actual market value. These examples clearly demonstrate how to calculate the percentage error using a simple formula and examples, showing the difference between approximate and exact values.Real-World Applications: Where Percent Error Matters
The utility of the percent error formula extends across a vast array of disciplines, proving its worth in scenarios where precision and accuracy are non-negotiable. See examples of using percent error in different contexts, such as guesses, measurements, and experiments.Percent Error in Scientific Experiments
In scientific research, percent error is a cornerstone for evaluating the reliability of experimental data. Whether it's in chemistry, physics, biology, or environmental science, experiments aim to either verify existing theories or discover new phenomena. When verifying a known value, percent error is the go-to metric. For instance, a chemistry student performing an experiment to determine the density of a known substance will compare their experimentally determined density to the substance's accepted theoretical density. A low percent error indicates that their experimental procedure was accurate and their measurements were precise. A high percent error, conversely, suggests that there might have been procedural errors, faulty equipment, or impurities in the sample, prompting a re-evaluation of the experimental setup. It helps scientists understand the difference between experimental values and expected values. Similarly, in physics, when calculating the acceleration due to gravity, students measure the time it takes for an object to fall a certain distance. They then compare their calculated 'g' value to the accepted value of 9.81 m/s². The percent error helps them assess the accuracy of their setup and calculations.Percent Error in Manufacturing and Quality Control
The stakes are often much higher in manufacturing and engineering, where small errors can lead to catastrophic failures, significant financial losses, or even endanger lives. Percent error is an indispensable tool for quality control and assurance. Consider the production of precision components, like those used in aerospace or medical devices. A bolt that is even a fraction of a millimeter too long or too short could compromise the integrity of an entire system. Manufacturers set strict tolerance levels, and the percent error of each produced component is meticulously checked against these standards. If the percent error exceeds a certain threshold, the component is rejected. This rigorous application of percent error ensures product reliability, safety, and adherence to design specifications. In pharmaceutical manufacturing, the precise dosage of active ingredients in medication is critical. A slight percent error in the concentration of a drug could render it ineffective or, worse, toxic. Quality control teams use percent error calculations to ensure that every batch of medication meets the exact formulation requirements. Find out why percentage error is important in scientific experiments and manufacturing processes.Everyday Examples of Estimation
While less formal, percent error concepts also apply to our daily lives, particularly when we make estimations. Percentages are an integral part of mathematics that we encounter regularly in various aspects of life. * **Budgeting:** When you estimate the cost of your groceries for the week, you can later calculate the percent error between your estimate and the actual amount spent. This helps you refine your budgeting skills. * **Time Management:** If you estimate how long a task will take, comparing it to the actual time spent reveals your percent error in time estimation, helping you plan more realistically in the future. * **Sports:** A sports analyst might estimate a player's performance statistics for an upcoming season. Comparing these estimates to the actual end-of-season stats involves calculating percent error to assess the accuracy of their predictions. These examples highlight how the percent error formula is not just an academic concept but a practical tool for assessing accuracy across a wide range of human activities.Navigating Negative Values and Absolute Value
One of the most common questions regarding the percent error formula revolves around negative values. What if the experimental value is less than the actual value? This is precisely why the absolute value function is an integral part of the formula. As previously noted, the formula uses `|Experimental Value - Actual Value|`. The vertical bars signify "absolute value." The absolute value of a number is its distance from zero on the number line, meaning it's always positive. For example: * If Experimental Value = 5 and Actual Value = 10, then (5 - 10) = -5. The absolute value is |-5| = 5. * If Experimental Value = 15 and Actual Value = 10, then (15 - 10) = 5. The absolute value is |5| = 5. In both cases, the absolute difference is 5. This ensures that the percent error always reflects the *magnitude* of the error, regardless of whether your measurement was an overestimate or an underestimate. A 5% error means you were off by 5% of the actual value, whether you were 5% too high or 5% too low. The direction of the error is usually less important than its size when discussing "error" in this context. If the direction *is* important, you would typically report the raw difference (Experimental - Actual) alongside the percent error, or use a different metric that retains the sign. Learn how to calculate the percentage error between approximate and exact values, using a formula with or without absolute value.Comparing Percent Error with Absolute and Relative Error
While often discussed together, absolute, relative, and percent error each offer a distinct perspective on the deviation of a measurement or estimate. Understanding their differences helps in choosing the most appropriate metric for a given situation. * **Absolute Error:** As discussed, this is the raw difference between the measured and actual value, expressed in the same units as the measurement. * **Pros:** Simple to calculate, gives the direct magnitude of the error. * **Cons:** Lacks context. A 1-meter error is huge for measuring a desk but negligible for measuring a highway. * **Relative Error:** This is the absolute error divided by the actual value. It's a dimensionless ratio or fraction. * **Pros:** Provides context by relating the error to the size of the actual value. Allows for comparison of accuracy across different scales. * **Cons:** Still a decimal or fraction, which might not be as intuitively understood by a general audience as a percentage. * **Percent Error:** This is the relative error multiplied by 100, expressed as a percentage. * **Pros:** Combines the contextual benefit of relative error with the ease of understanding of percentages. It's widely used and intuitively graspable by a broad audience. * **Cons:** Can sometimes be misinterpreted if the actual value is very small or zero (division by zero is undefined, and small denominators can lead to disproportionately large percent errors). In summary, absolute error tells you "how much" you were off, relative error tells you "how much relative to the true value" you were off, and percent error tells you "what percentage" of the true value you were off by. Percent error is the most commonly reported and understood metric because it provides a clear, standardized, and easily comparable measure of accuracy. See an example calculation and compare percent error with absolute and relative error.Tools and Resources for Calculating Percent Error
While the percent error formula is simple enough to calculate by hand or with a basic calculator, several tools and resources can streamline the process, especially when dealing with multiple calculations or complex datasets. * **Online Calculators:** Numerous websites offer free percent error calculators. You simply input your experimental and actual values, and the calculator instantly provides the percent error, often alongside absolute and relative error. This free percent error calculator computes the percentage error between an observed value and the true value of a measurement. They are convenient for quick checks and for verifying manual calculations. * **Spreadsheet Software (e.g., Microsoft Excel, Google Sheets):** For scientists, engineers, or anyone working with large sets of data, spreadsheet software is invaluable. You can set up columns for experimental value, actual value, and then use formulas to automatically calculate the percent error for each data point. This allows for efficient analysis and visualization of errors across multiple trials or measurements. Guide to percent error formula, here we will learn how to calculate percent error with examples, calculator and downloadable excel template. * **Scientific Calculators:** Most scientific calculators have an absolute value function, making manual calculations straightforward. * **Educational Resources:** Websites like Byju's and others provide thorough explanations, solved examples, and guides on how to calculate percentage error in a few easy steps. These resources are excellent for learning and reinforcing understanding. Stay tuned with byju’s for more such interesting articles. Leveraging these tools can significantly enhance efficiency and accuracy in your calculations, allowing you to focus more on interpreting the results rather than just crunching numbers.Common Pitfalls and Best Practices
While calculating percent error is straightforward, certain pitfalls can lead to incorrect results or misinterpretations. Adhering to best practices ensures accuracy and meaningful analysis. **Common Pitfalls:** 1. **Incorrectly Identifying Values:** A frequent mistake is mixing up the experimental and actual values, or using the wrong value as the denominator. Always ensure `Actual Value` is in the denominator. 2. **Forgetting Absolute Value:** Neglecting to take the absolute value of the difference will result in a negative percent error if the experimental value is lower than the actual value, which can be confusing or misleading as error magnitude is typically positive. 3. **Division by Zero:** If the actual value is zero, the percent error formula becomes undefined. In such rare cases, percent error cannot be calculated, and absolute error might be the only meaningful metric. 4. **Misinterpreting "Good" Percent Error:** What constitutes an "acceptable" percent error varies greatly by field and context. A 1% error might be excellent in a complex chemical synthesis but disastrous in precision engineering. Always consider the context and industry standards. 5. **Ignoring Significant Figures:** When performing calculations, be mindful of the significant figures of your measurements to ensure your final percent error reflects the precision of your input data. **Best Practices:** 1. **Double-Check Your Values:** Before calculating, confirm that you have correctly identified the experimental and actual values. 2. **Always Use Absolute Value:** Make it a habit to apply the absolute value to the difference between the experimental and actual values. 3. **Understand the Context:** Always interpret the percent error within the specific context of your experiment or application. What are the acceptable tolerances? What are the implications of the error? 4. **Report Clearly:** When presenting results, clearly state the experimental value, actual value, and the calculated percent error. If relevant, also mention absolute and relative errors. 5. **Identify Error Sources:** A high percent error should prompt an investigation into potential sources of error, such as equipment calibration issues, measurement technique inconsistencies, or environmental factors. This iterative process is crucial for improving experimental design and accuracy. 6. **Use Appropriate Tools:** Leverage online calculators or spreadsheet software for efficiency and to minimize manual calculation errors, especially with large datasets. By understanding and avoiding these pitfalls, and by adopting best practices, you can ensure that your use of the percent error formula is accurate, insightful, and contributes effectively to your analysis and decision-making.Conclusion
The percent error formula stands as a fundamental pillar in the pursuit of accuracy and precision across scientific, industrial, and even everyday applications. It provides a universally understood metric to quantify the relative difference between an observed or estimated value and a true, accepted value. By mastering this simple yet powerful formula – `Percent Error = (|Experimental Value - Actual Value| / Actual Value) × 100%` – you gain the ability to critically evaluate data, identify potential discrepancies, and ultimately enhance the reliability of your work. From the meticulous measurements in a laboratory to the stringent quality control in manufacturing, and even in our personal estimations, understanding how to calculate and interpret percent error is an indispensable skill. It not only highlights the magnitude of an error but also contextualizes it, allowing for meaningful comparisons and informed decision-making. As we've seen, while absolute and relative errors offer different perspectives, percent error combines their strengths into an easily digestible percentage. We encourage you to practice applying the percent error formula using the examples provided and to explore its relevance in your own field or daily life. The journey to greater precision begins with understanding how to measure deviation. What are your thoughts on the importance of percent error in your field? Share your experiences or questions in the comments below! If you found this guide helpful, consider sharing it with others who might benefit, and explore our other articles for more insights into essential scientific and mathematical concepts.- Antoni Grisman
- Jenisa Brazil
- Oj Simpson Social Media
- Madame Clairevoyant The Cut
- Asian Hotwife Ashley

How to Calculate the Percentage Error (Pictures and Examples

How to Calculate Percent Error?- Concept and Calculation, Meaning
Percent Error Formula | How to Calculate Percent Error | Examples